相信大家在石材工程施工过程中都会遇到一些几何尺寸不知怎么计算或者没有找到简单的办法而没有精确的计算。我在工作中就经常有朋友打电话或者微信来让我来帮忙计算,觉得应该还有很多人需要就整理出来,每个公式都有详细计算步骤,希望朋友们能按照步骤照做一次可以验证验证和加深一下印象。
一、多边形的内角和:
任何≥3边多边形的内角和公式:(n-2)×180°
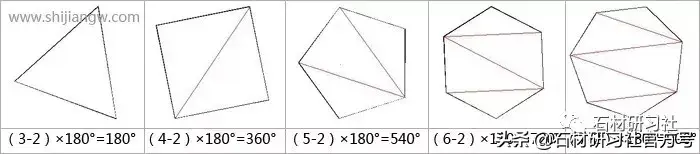
解析说明:三角形的内角和是180°,只要看一个多边形能分成几个三角形就是几乘以180。
二、三角形面积和周长:
直角三角形的三边关系:直角1边2+直角2边2=斜边2,三角形面积=底×高÷2(适用于任何三角形)
应用案例解析:比如电动自动门的拉门洞,已知短边、长边、高度,求斜边长度?
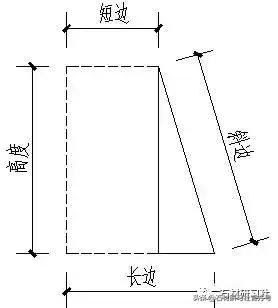
1、(长边-短边)*(长边-短边)+高度*高度=得到数
2、√得到数=就是斜边的长度
三角函数在板材切角中的应用:工程中利用三角函数可以正确无误的切角
三、 四边形面积和周长、柱的面积和体积:
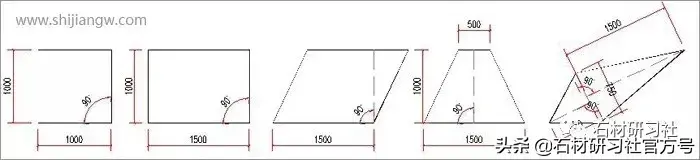
1、四条边等长(正方形,4角皆是90°):周长=边长×4;面积=边长×边长
2、四条边两两等长(长方形,4角皆是90°):周长=(长边+短边)×2;面积=长边×短边
3、四条边两两等长(平行四边形,4角皆非90°):周长=(长边+短边)×2;面积 =底×高
4、四条边两等两不等比如梯形:周长=上边+下边+侧边×2;面积=(上底+下底)×高÷2
5、四条边均不等长(平行四边形,4角皆非90°):周长=1边长+2边长+3边长+4边长;面积=三角形面积+三角形面积
(解析说明:我的个人建议是把四边形作对角线,化四边形为三角形分别计算两个三角形的面积,如果利用海伦公式和三角函数会比较麻烦,我们毕竟不是学生应付考试,只要实际测量时直接量出三角形的长边和高)
以上所有四边为基础的柱的侧面积:四边形周长×高;体积:四边形面积×高
四、圆的周长、面积
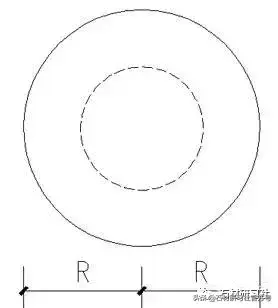
圆截面积计算公式:S = 3.14×R ×R (S是截面积,R是半径)
举例:一大理石拼花的直径是1.5, 求其面积:0.75× 0.75× 3.14=0.5625× 3.14= 1.76625 提示:圆环面积=大圆面积-小圆面积
圆周长计算公式:L=(R+R)× 3.14
举例:一圆形花池的直径是1.5, 求出其圆的周长再乘以高度就是花池碧的石材面积
五、椭圆的周长、面积
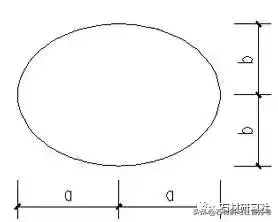
椭圆的周长、面积 椭圆的周长:L=2× 3.14×b+4(a-b)
椭圆的面积:S=3.14×a×b
六、已知弧形的长度和玄的高度,求圆的半径
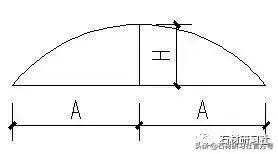
圆弧的半径:R=(A*A+H*H)/2/H
举例:已知弧1的半径和弧长求弧2的弧长
比如弧形墙的弧长和玄长我们现场是很容易量出来的,能算出半径R1,那R2就墙体的外半径+石材完成面出墙尺寸,通过公式就能计算出石材干挂完成后的总弧长。
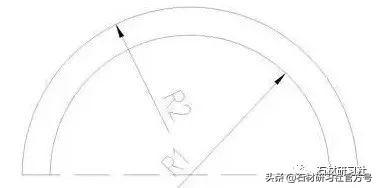
弧2长度=弧1长度*R2/R1
举例:知道玄高和玄长,怎么求半径和弧长
假如这是一个需要铺装的现场能测量到尺寸,想求出那条弧线的半径和弧长
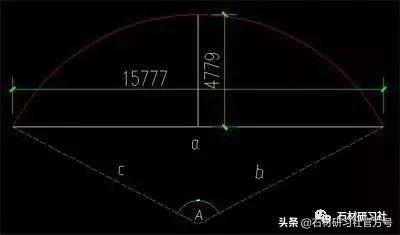
首先求半径的公式(a*a+h*h)/2/h(公式中的a是半条玄长)
代入实际尺寸则为:
半径=(7888.5*7888.5+4779*4779)/2/4779=8900
求弧长的推理过程
首先正圆周长很容易了,L=(R+R)× 3.14=(8.9+8.9)*3.14=55.89
注意这个周长是整个圆的周长,我要求其中一段,就要首先虚拟一个A夹角(圆心),目前已知道这个虚拟的三角形的三条边为15777和8900和8900,根据三角形的余玄定理求出这个夹角度数
公式为:cosa=(b^2+c^2-a^2)/2bc
代入实际尺寸则为:(8.9*8.9*2-15.777*15.777)/2/8.9/8.9=-0.57
再利用计算器反余玄-0.57约等于124.75度
那么弧长=124.75/360*55.89(整圆周长)=19.37米。(面积同理)
七、圆锥、圆台:

圆锥的体积=底面积×高÷3
圆锥的侧面积=S=RL÷2
(R为圆锥体底面圆的周长,L为圆锥的顶点到圆锥的底面圆周之间的距离)
解析说明:圆锥侧面展开以后就是一个扇形,扇形的弧长就是圆锥底的周长。
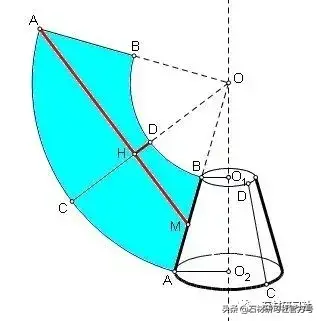
其实圆锥我们可能不常用到,更常用到的是圆台(比如上下不同径的圆柱)
圆台的体积公式: V=3.14×h×(R2+r2+Rr)÷3
(其中r是上底面半径,R是下底面半径)
圆台的底面和顶面近似时,圆台体积可近似为:圆台的底面面积S1加顶面面积S2除以2的平均面积1/2(S1+S2)的一个圆柱体乘以高h,即V=(S1+s2)×h÷2
圆台的侧面积公式:S=πr2+πR2+πRl+πrl=π(r2+R2+Rl+rl)
π=3.1415 r:上底半径、R:下底半径、h:高、l:母线=根号下[(R-r)2+h2]
